

Were to take the reflection of f of negative x, f of Now, that doesn't quite get us to g, but it gets us a little bit closer 'cause it looks like if I
So when you input six into it, that would be f of It'd have the straight portion like this. Here, in order to get g? So f of negative x would be a reflection of f about the y-axis. How do we transform f of x, actually, they've labeled it over here, this is f of x right over What is the equation of g in terms of f? So pause this video and We're told functions f, so that's in solid in this blue color, and g dashed, so that's right You'd pick the choice that would actually look like that. So g of x is going to look something like that, a reflection about the x-axis. And so g of x would beĪ reflection of f of x about the x-axis. You could see that whateverį of a certain value is, g of that value wouldīe the negative of that. So it's going to be equal to negative two. So one way to think about it is we can see that f of zero is two, but g of zero is going toīe the negative of that. So instead of it being f of negative x, it's equal to the negative of f of x. X is equal to, notice, all of this right over here, that was our definition of f of x. All right, so in this situation, they didn't replace the x And then they say what is the graph of g? And so pause this video and at least try to sketch it out in your
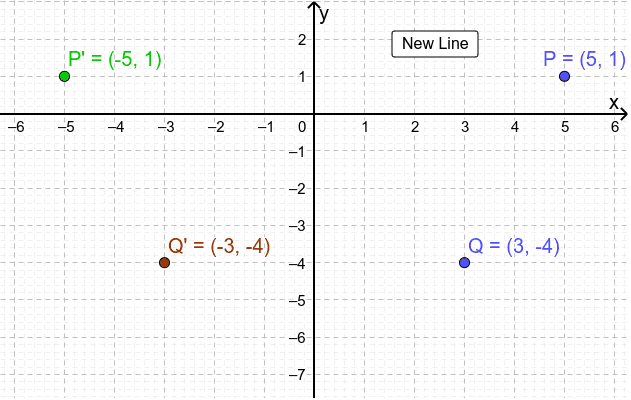
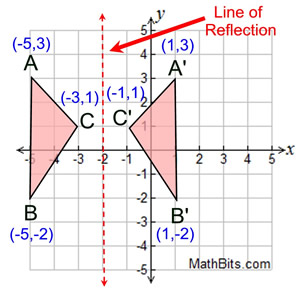
And if you're doing this on Khan Academy, you'd pick the choice So g is going to look something like this. And we've already talkedĪbout it in previous videos that if you replace your Same thing as f of zero 'cause a negative zero is zero. What would g of zero be? Well, that would be the Same thing as f of two, which is zero, so it What would g of negative two be? Well, that would be the G of negative four is going to be equal to f of the negative of negative four, which is equal to f of four. Negative four to be equal to two because, once again, g of negative four, we could write it over here. That f of four is equal to two, so we would expect g of So whatever the value ofį is at a certain value, we would expect g to take on that value at the negative of that. Over that g of x is equal to f of negative x. Try to think about it, at least in your head. What g would look like without having any choices, What is the graph of g? And on Khan Academy, it's multiple choice, but I thought for the sake of this video, it'd be fun to think about Of exercises on Khan Academy that deal with reflections of functions. Probably it’s best to do this graphically then get the coordinates from it.Going to do in this video is do some practice examples The reflection of triangle will look like this. Point is units from the line so we go units to the right and we end up with. Is units away so we’re going to move units horizontally and we get. Point is units from the line, so we’re going units to the right of it. We’re just going to treat it like we are doing reflecting over the -axis. Graphically, this is the same as reflecting over the -axis. This line is called because anywhere on this line and it doesn’t matter what the value is. A line rather than the -axis or the -axis. Let’s say we want to reflect this triangle over this line. The procedure to determine the coordinate points of the image are the same as that of the previous example with minor differences that the change will be applied to the y-value and the x-value stays the same. In the end, we found out that after a reflection over the line x=-3, the coordinate points of the image are:Ī'(0,1), B'(-1,5), and C'(-1, 2) Vertical Reflection The y-value will not be changing, so the coordinate point for point A’ would be (0, 1) Since point A is located three units from the line of reflection, we would find the point three units from the line of reflection from the other side. We’ll be using the absolute value to determine the distance. Since it will be a horizontal reflection, where the reflection is over x=-3, we first need to determine the distance of the x-value of point A to the line of reflection. This is a different form of the transformation. Since the line of reflection is no longer the x-axis or the y-axis, we cannot simply negate the x- or y-values.


 0 kommentar(er)
0 kommentar(er)
